Трапеція
Трапе́ція — це чотирикутник, дві протилежні сторони якого паралельні. Паралельні сторони називаються основами трапеції (сторони AB та DC на малюнку). Інші сторони називаються бічними сторонами (сторони AD та CB).
· Рівнобічна трапеція, тобто трапеція у якої бічні сторони рівні.
· Прямокутна трапеція — це трапеція у якої два кута прямі.
· Різностороння трапеція, у якої всі сторони різні.
Відрізок, який сполучає середини бічних сторін, називається середньою лінією трапеції. Середня лінія паралельна основам трапеції, а її довжина дорівнює їх півсумі:
Основні види трапецій
Трапецію називають прямокутною, якщо у неї два суміжних кути дорівнюють 90°.
Гострою називається трапеція у якої кути, прилеглі до більшої основи гострі (менше 90°).
Трапецію називають рівнобічною, якщо її бічні сторони та кути, прилеглі до більшої основи, рівні. Ця трапеція має осьову симетрію.
Тупою називається трапеція, у якої один із кутів, прилеглих до більшої основи, тупий (більше 90°).
Трапеція з двома парами паралельних сторін називається паралелограмом. Паралелограм має дві осьові симметрії.
У широкому сенсі, всі паралелограми (включаючи ромби, прямокутники і квадрати) є трапеції. Прямокутники мають дзеркальну симетрію по середині ребер; ромби мають дзеркальну симетрію на вершинах, а квадрати мають дзеркальну симетрію з обох середніх ребер і вершин.
Дотичною називається трапеція, в яку має вписане коло.
Властивості
Для будь-якого опуклого чотирикутника такі властивості еквівалентні, і кожна передбачає, що чотирикутник є трапецією:
· Сума двох суміжних кутів дорівнює 180 градусів.
· Кут між однією основою і діагоналлю дорівнює куту між іншою основою та тією ж діагоналлю (внутрішні різносторонні кути рівні).
· Середня лінія трапеції паралельна основам і дорівнює їх півсумі.
· В трапецію можна вписати коло, якщо сума основ трапеції дорівнює сумі її бічних сторін.
· Точка перетину діагоналей трапеції, точка перетину продовжень її бічних сторін та середини основ лежать на одній прямій.
· Трикутники, утворені відрізками діагоналей та основами трапеції, подібні.
· Трикутники, утворені відрізками діагоналей та бічними сторонами трапеції, мають однакову площу.
· Відрізок, що з'єднує середини діагоналей, дорівнює піврізниці основ і лежить на середній лінії.
· Бісектриса будь-якого кута трапеції відтинає на її основі (або продовженні) відрізок, рівний бічній стороні.
· Якщо сума кутів при будь-якій основі трапеції дорівнює 90°, то відрізок, що з'єднує середини основ, дорівнює їх піврізниці.
· Якщо сума основ трапеції дорівнює сумі її бічних сторін, то в таку трапецію можна вписати коло, і навпаки.
· Будь-яку трапецію можна побудувати за довжинами чотирьох сторін.
· В рівнобічній трапеції кути при основі, а також діагоналі рівні.
· Навколо рівнобічної трапеції можна описати коло.
Висота трапеції
Висота — перпендикулярна відстань між основами. У разі, коли дві основи мають різну довжину (а ≠ b), висота трапеції може бути визначена через довжини чотирьох сторін за формулою:
,

де a, b — основи трапеції, а c і d — бокові сторони. Формула висоти трапеції, виражена через бокові сторони та кути, що прилеглі до більшої основи:
Формула висоти трапеції, виражена через діагоналі та кути між ними:
Формула висоти трапеції, виражена через площу:
 , де S — площа трапеції, m — середня лінія.
, де S — площа трапеції, m — середня лінія.
 , де S — площа трапеції, m — середня лінія.
, де S — площа трапеції, m — середня лінія.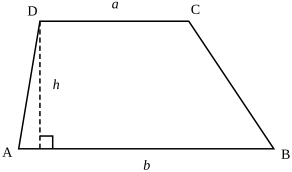


Немає коментарів:
Дописати коментар